diff --git a/solution/1200-1299/1277.Count Square Submatrices with All Ones/README.md b/solution/1200-1299/1277.Count Square Submatrices with All Ones/README.md
index 03ef99ee958af..602ef655eca41 100644
--- a/solution/1200-1299/1277.Count Square Submatrices with All Ones/README.md
+++ b/solution/1200-1299/1277.Count Square Submatrices with All Ones/README.md
@@ -33,7 +33,7 @@ tags:
[0,1,1,1]
]
输出:15
-解释:
+解释:
边长为 1 的正方形有 10 个。
边长为 2 的正方形有 4 个。
边长为 3 的正方形有 1 个。
@@ -42,7 +42,7 @@ tags:
示例 2:
-输入:matrix =
+输入:matrix =
[
[1,0,1],
[1,1,0],
@@ -50,7 +50,7 @@ tags:
]
输出:7
解释:
-边长为 1 的正方形有 6 个。
+边长为 1 的正方形有 6 个。
边长为 2 的正方形有 1 个。
正方形的总数 = 6 + 1 = 7.
@@ -71,7 +71,20 @@ tags:
-### 方法一
+### 方法一:动态规划
+
+我们定义 $f[i][j]$ 为以 $(i,j)$ 为右下角的正方形子矩阵的边长,初始时 $f[i][j] = 0$,答案为 $\sum_{i,j} f[i][j]$。
+
+考虑 $f[i][j]$ 如何进行状态转移。
+
+- 当 $\text{matrix}[i][j] = 0$ 时,有 $f[i][j] = 0$。
+- 当 $\text{matrix}[i][j] = 1$ 时,状态 $f[i][j]$ 的值取决于其上、左、左上三个位置的值:
+ - 如果 $i = 0$ 或 $j = 0$,则 $f[i][j] = 1$。
+ - 否则 $f[i][j] = \min(f[i-1][j-1], f[i-1][j], f[i][j-1]) + 1$。
+
+答案为 $\sum_{i,j} f[i][j]$。
+
+时间复杂度 $O(m \times n)$,空间复杂度 $O(m \times n)$。其中 $m$ 和 $n$ 分别为矩阵的行数和列数。
@@ -133,11 +146,14 @@ public:
vector> f(m, vector(n));
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
- if (matrix[i][j] == 0) continue;
- if (i == 0 || j == 0)
+ if (matrix[i][j] == 0) {
+ continue;
+ }
+ if (i == 0 || j == 0) {
f[i][j] = 1;
- else
+ } else {
f[i][j] = min(f[i - 1][j - 1], min(f[i - 1][j], f[i][j - 1])) + 1;
+ }
ans += f[i][j];
}
}
@@ -176,18 +192,22 @@ func countSquares(matrix [][]int) int {
```ts
function countSquares(matrix: number[][]): number {
- const [m, n] = [matrix.length, matrix[0].length];
- const f = Array.from({ length: m }, () => Array(n));
- const dfs = (i: number, j: number): number => {
- if (i === m || j === n || !matrix[i][j]) return 0;
- f[i][j] ??= 1 + Math.min(dfs(i + 1, j), dfs(i, j + 1), dfs(i + 1, j + 1));
- return f[i][j];
- };
+ const m = matrix.length;
+ const n = matrix[0].length;
+ const f: number[][] = Array.from({ length: m }, () => Array(n).fill(0));
let ans = 0;
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
- ans += dfs(i, j);
+ if (matrix[i][j] === 0) {
+ continue;
+ }
+ if (i === 0 || j === 0) {
+ f[i][j] = 1;
+ } else {
+ f[i][j] = Math.min(f[i - 1][j - 1], Math.min(f[i - 1][j], f[i][j - 1])) + 1;
+ }
+ ans += f[i][j];
}
}
@@ -195,26 +215,92 @@ function countSquares(matrix: number[][]): number {
}
```
+#### Rust
+
+```rust
+impl Solution {
+ pub fn count_squares(matrix: Vec>) -> i32 {
+ let m = matrix.len();
+ let n = matrix[0].len();
+ let mut f = vec![vec![0; n]; m];
+ let mut ans = 0;
+
+ for i in 0..m {
+ for j in 0..n {
+ if matrix[i][j] == 0 {
+ continue;
+ }
+ if i == 0 || j == 0 {
+ f[i][j] = 1;
+ } else {
+ f[i][j] = std::cmp::min(f[i - 1][j - 1], std::cmp::min(f[i - 1][j], f[i][j - 1])) + 1;
+ }
+ ans += f[i][j];
+ }
+ }
+
+ ans
+ }
+}
+```
+
#### JavaScript
```js
-function countSquares(matrix) {
- const [m, n] = [matrix.length, matrix[0].length];
- const f = Array.from({ length: m }, () => Array(n));
- const dfs = (i, j) => {
- if (i === m || j === n || !matrix[i][j]) return 0;
- f[i][j] ??= 1 + Math.min(dfs(i + 1, j), dfs(i, j + 1), dfs(i + 1, j + 1));
- return f[i][j];
- };
+/**
+ * @param {number[][]} matrix
+ * @return {number}
+ */
+var countSquares = function (matrix) {
+ const m = matrix.length;
+ const n = matrix[0].length;
+ const f = Array.from({ length: m }, () => Array(n).fill(0));
let ans = 0;
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
- ans += dfs(i, j);
+ if (matrix[i][j] === 0) {
+ continue;
+ }
+ if (i === 0 || j === 0) {
+ f[i][j] = 1;
+ } else {
+ f[i][j] = Math.min(f[i - 1][j - 1], Math.min(f[i - 1][j], f[i][j - 1])) + 1;
+ }
+ ans += f[i][j];
}
}
return ans;
+};
+```
+
+#### C#
+
+```cs
+public class Solution {
+ public int CountSquares(int[][] matrix) {
+ int m = matrix.Length;
+ int n = matrix[0].Length;
+ int[,] f = new int[m, n];
+ int ans = 0;
+
+ for (int i = 0; i < m; i++) {
+ for (int j = 0; j < n; j++) {
+ if (matrix[i][j] == 0) {
+ continue;
+ }
+ if (i == 0 || j == 0) {
+ f[i, j] = 1;
+ } else {
+ f[i, j] = Math.Min(f[i - 1, j - 1], Math.Min(f[i - 1, j], f[i, j - 1])) + 1;
+ }
+ ans += f[i, j];
+ }
+ }
+
+ return ans;
+ }
}
```
diff --git a/solution/1200-1299/1277.Count Square Submatrices with All Ones/README_EN.md b/solution/1200-1299/1277.Count Square Submatrices with All Ones/README_EN.md
index 2df7a529fba59..d21234d30f959 100644
--- a/solution/1200-1299/1277.Count Square Submatrices with All Ones/README_EN.md
+++ b/solution/1200-1299/1277.Count Square Submatrices with All Ones/README_EN.md
@@ -33,7 +33,7 @@ tags:
[0,1,1,1]
]
Output: 15
-Explanation:
+Explanation:
There are 10 squares of side 1.
There are 4 squares of side 2.
There is 1 square of side 3.
@@ -43,16 +43,16 @@ Total number of squares = 10 + 4 + 1 = 15.
Example 2:
-Input: matrix =
+Input: matrix =
[
[1,0,1],
[1,1,0],
[1,1,0]
]
Output: 7
-Explanation:
-There are 6 squares of side 1.
-There is 1 square of side 2.
+Explanation:
+There are 6 squares of side 1.
+There is 1 square of side 2.
Total number of squares = 6 + 1 = 7.
@@ -71,7 +71,20 @@ Total number of squares = 6 + 1 = 7.
-### Solution 1
+### Solution 1: Dynamic Programming
+
+We define $f[i][j]$ as the side length of the square submatrix with $(i,j)$ as the bottom-right corner. Initially $f[i][j] = 0$, and the answer is $\sum_{i,j} f[i][j]$.
+
+Consider how to perform state transition for $f[i][j]$.
+
+- When $\text{matrix}[i][j] = 0$, we have $f[i][j] = 0$.
+- When $\text{matrix}[i][j] = 1$, the value of state $f[i][j]$ depends on the values of the three positions above, left, and top-left:
+ - If $i = 0$ or $j = 0$, then $f[i][j] = 1$.
+ - Otherwise $f[i][j] = \min(f[i-1][j-1], f[i-1][j], f[i][j-1]) + 1$.
+
+The answer is $\sum_{i,j} f[i][j]$.
+
+Time complexity $O(m \times n)$, space complexity $O(m \times n)$. Where $m$ and $n$ are the number of rows and columns of the matrix respectively.
@@ -133,11 +146,14 @@ public:
vector> f(m, vector(n));
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
- if (matrix[i][j] == 0) continue;
- if (i == 0 || j == 0)
+ if (matrix[i][j] == 0) {
+ continue;
+ }
+ if (i == 0 || j == 0) {
f[i][j] = 1;
- else
+ } else {
f[i][j] = min(f[i - 1][j - 1], min(f[i - 1][j], f[i][j - 1])) + 1;
+ }
ans += f[i][j];
}
}
@@ -176,18 +192,22 @@ func countSquares(matrix [][]int) int {
```ts
function countSquares(matrix: number[][]): number {
- const [m, n] = [matrix.length, matrix[0].length];
- const f = Array.from({ length: m }, () => Array(n));
- const dfs = (i: number, j: number): number => {
- if (i === m || j === n || !matrix[i][j]) return 0;
- f[i][j] ??= 1 + Math.min(dfs(i + 1, j), dfs(i, j + 1), dfs(i + 1, j + 1));
- return f[i][j];
- };
+ const m = matrix.length;
+ const n = matrix[0].length;
+ const f: number[][] = Array.from({ length: m }, () => Array(n).fill(0));
let ans = 0;
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
- ans += dfs(i, j);
+ if (matrix[i][j] === 0) {
+ continue;
+ }
+ if (i === 0 || j === 0) {
+ f[i][j] = 1;
+ } else {
+ f[i][j] = Math.min(f[i - 1][j - 1], Math.min(f[i - 1][j], f[i][j - 1])) + 1;
+ }
+ ans += f[i][j];
}
}
@@ -195,26 +215,92 @@ function countSquares(matrix: number[][]): number {
}
```
+#### Rust
+
+```rust
+impl Solution {
+ pub fn count_squares(matrix: Vec>) -> i32 {
+ let m = matrix.len();
+ let n = matrix[0].len();
+ let mut f = vec![vec![0; n]; m];
+ let mut ans = 0;
+
+ for i in 0..m {
+ for j in 0..n {
+ if matrix[i][j] == 0 {
+ continue;
+ }
+ if i == 0 || j == 0 {
+ f[i][j] = 1;
+ } else {
+ f[i][j] = std::cmp::min(f[i - 1][j - 1], std::cmp::min(f[i - 1][j], f[i][j - 1])) + 1;
+ }
+ ans += f[i][j];
+ }
+ }
+
+ ans
+ }
+}
+```
+
#### JavaScript
```js
-function countSquares(matrix) {
- const [m, n] = [matrix.length, matrix[0].length];
- const f = Array.from({ length: m }, () => Array(n));
- const dfs = (i, j) => {
- if (i === m || j === n || !matrix[i][j]) return 0;
- f[i][j] ??= 1 + Math.min(dfs(i + 1, j), dfs(i, j + 1), dfs(i + 1, j + 1));
- return f[i][j];
- };
+/**
+ * @param {number[][]} matrix
+ * @return {number}
+ */
+var countSquares = function (matrix) {
+ const m = matrix.length;
+ const n = matrix[0].length;
+ const f = Array.from({ length: m }, () => Array(n).fill(0));
let ans = 0;
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
- ans += dfs(i, j);
+ if (matrix[i][j] === 0) {
+ continue;
+ }
+ if (i === 0 || j === 0) {
+ f[i][j] = 1;
+ } else {
+ f[i][j] = Math.min(f[i - 1][j - 1], Math.min(f[i - 1][j], f[i][j - 1])) + 1;
+ }
+ ans += f[i][j];
}
}
return ans;
+};
+```
+
+#### C#
+
+```cs
+public class Solution {
+ public int CountSquares(int[][] matrix) {
+ int m = matrix.Length;
+ int n = matrix[0].Length;
+ int[,] f = new int[m, n];
+ int ans = 0;
+
+ for (int i = 0; i < m; i++) {
+ for (int j = 0; j < n; j++) {
+ if (matrix[i][j] == 0) {
+ continue;
+ }
+ if (i == 0 || j == 0) {
+ f[i, j] = 1;
+ } else {
+ f[i, j] = Math.Min(f[i - 1, j - 1], Math.Min(f[i - 1, j], f[i, j - 1])) + 1;
+ }
+ ans += f[i, j];
+ }
+ }
+
+ return ans;
+ }
}
```
diff --git a/solution/1200-1299/1277.Count Square Submatrices with All Ones/Solution.cpp b/solution/1200-1299/1277.Count Square Submatrices with All Ones/Solution.cpp
index 75f9da14ffd31..49aca7700e297 100644
--- a/solution/1200-1299/1277.Count Square Submatrices with All Ones/Solution.cpp
+++ b/solution/1200-1299/1277.Count Square Submatrices with All Ones/Solution.cpp
@@ -6,14 +6,17 @@ class Solution {
vector> f(m, vector(n));
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
- if (matrix[i][j] == 0) continue;
- if (i == 0 || j == 0)
+ if (matrix[i][j] == 0) {
+ continue;
+ }
+ if (i == 0 || j == 0) {
f[i][j] = 1;
- else
+ } else {
f[i][j] = min(f[i - 1][j - 1], min(f[i - 1][j], f[i][j - 1])) + 1;
+ }
ans += f[i][j];
}
}
return ans;
}
-};
\ No newline at end of file
+};
diff --git a/solution/1200-1299/1277.Count Square Submatrices with All Ones/Solution.cs b/solution/1200-1299/1277.Count Square Submatrices with All Ones/Solution.cs
new file mode 100644
index 0000000000000..608c1a65ada57
--- /dev/null
+++ b/solution/1200-1299/1277.Count Square Submatrices with All Ones/Solution.cs
@@ -0,0 +1,24 @@
+public class Solution {
+ public int CountSquares(int[][] matrix) {
+ int m = matrix.Length;
+ int n = matrix[0].Length;
+ int[,] f = new int[m, n];
+ int ans = 0;
+
+ for (int i = 0; i < m; i++) {
+ for (int j = 0; j < n; j++) {
+ if (matrix[i][j] == 0) {
+ continue;
+ }
+ if (i == 0 || j == 0) {
+ f[i, j] = 1;
+ } else {
+ f[i, j] = Math.Min(f[i - 1, j - 1], Math.Min(f[i - 1, j], f[i, j - 1])) + 1;
+ }
+ ans += f[i, j];
+ }
+ }
+
+ return ans;
+ }
+}
diff --git a/solution/1200-1299/1277.Count Square Submatrices with All Ones/Solution.js b/solution/1200-1299/1277.Count Square Submatrices with All Ones/Solution.js
index 422c84c168eff..2dda7776c0e02 100644
--- a/solution/1200-1299/1277.Count Square Submatrices with All Ones/Solution.js
+++ b/solution/1200-1299/1277.Count Square Submatrices with All Ones/Solution.js
@@ -1,18 +1,26 @@
-function countSquares(matrix) {
- const [m, n] = [matrix.length, matrix[0].length];
- const f = Array.from({ length: m }, () => Array(n));
- const dfs = (i, j) => {
- if (i === m || j === n || !matrix[i][j]) return 0;
- f[i][j] ??= 1 + Math.min(dfs(i + 1, j), dfs(i, j + 1), dfs(i + 1, j + 1));
- return f[i][j];
- };
+/**
+ * @param {number[][]} matrix
+ * @return {number}
+ */
+var countSquares = function (matrix) {
+ const m = matrix.length;
+ const n = matrix[0].length;
+ const f = Array.from({ length: m }, () => Array(n).fill(0));
let ans = 0;
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
- ans += dfs(i, j);
+ if (matrix[i][j] === 0) {
+ continue;
+ }
+ if (i === 0 || j === 0) {
+ f[i][j] = 1;
+ } else {
+ f[i][j] = Math.min(f[i - 1][j - 1], Math.min(f[i - 1][j], f[i][j - 1])) + 1;
+ }
+ ans += f[i][j];
}
}
return ans;
-}
+};
diff --git a/solution/1200-1299/1277.Count Square Submatrices with All Ones/Solution.rs b/solution/1200-1299/1277.Count Square Submatrices with All Ones/Solution.rs
new file mode 100644
index 0000000000000..57a7faf6f20f7
--- /dev/null
+++ b/solution/1200-1299/1277.Count Square Submatrices with All Ones/Solution.rs
@@ -0,0 +1,25 @@
+impl Solution {
+ pub fn count_squares(matrix: Vec>) -> i32 {
+ let m = matrix.len();
+ let n = matrix[0].len();
+ let mut f = vec![vec![0; n]; m];
+ let mut ans = 0;
+
+ for i in 0..m {
+ for j in 0..n {
+ if matrix[i][j] == 0 {
+ continue;
+ }
+ if i == 0 || j == 0 {
+ f[i][j] = 1;
+ } else {
+ f[i][j] =
+ std::cmp::min(f[i - 1][j - 1], std::cmp::min(f[i - 1][j], f[i][j - 1])) + 1;
+ }
+ ans += f[i][j];
+ }
+ }
+
+ ans
+ }
+}
diff --git a/solution/1200-1299/1277.Count Square Submatrices with All Ones/Solution.ts b/solution/1200-1299/1277.Count Square Submatrices with All Ones/Solution.ts
index 15f02bbe04c42..985938d954e55 100644
--- a/solution/1200-1299/1277.Count Square Submatrices with All Ones/Solution.ts
+++ b/solution/1200-1299/1277.Count Square Submatrices with All Ones/Solution.ts
@@ -1,16 +1,20 @@
function countSquares(matrix: number[][]): number {
- const [m, n] = [matrix.length, matrix[0].length];
- const f = Array.from({ length: m }, () => Array(n));
- const dfs = (i: number, j: number): number => {
- if (i === m || j === n || !matrix[i][j]) return 0;
- f[i][j] ??= 1 + Math.min(dfs(i + 1, j), dfs(i, j + 1), dfs(i + 1, j + 1));
- return f[i][j];
- };
+ const m = matrix.length;
+ const n = matrix[0].length;
+ const f: number[][] = Array.from({ length: m }, () => Array(n).fill(0));
let ans = 0;
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
- ans += dfs(i, j);
+ if (matrix[i][j] === 0) {
+ continue;
+ }
+ if (i === 0 || j === 0) {
+ f[i][j] = 1;
+ } else {
+ f[i][j] = Math.min(f[i - 1][j - 1], Math.min(f[i - 1][j], f[i][j - 1])) + 1;
+ }
+ ans += f[i][j];
}
}
diff --git a/solution/2300-2399/2348.Number of Zero-Filled Subarrays/README_EN.md b/solution/2300-2399/2348.Number of Zero-Filled Subarrays/README_EN.md
index 65887ef4f9bf5..a1d563d27c336 100644
--- a/solution/2300-2399/2348.Number of Zero-Filled Subarrays/README_EN.md
+++ b/solution/2300-2399/2348.Number of Zero-Filled Subarrays/README_EN.md
@@ -29,7 +29,7 @@ tags:
Input: nums = [1,3,0,0,2,0,0,4]
Output: 6
-Explanation:
+Explanation:
There are 4 occurrences of [0] as a subarray.
There are 2 occurrences of [0,0] as a subarray.
There is no occurrence of a subarray with a size more than 2 filled with 0. Therefore, we return 6.
diff --git a/solution/3600-3699/3656.Determine if a Simple Graph Exists/README.md b/solution/3600-3699/3656.Determine if a Simple Graph Exists/README.md
new file mode 100644
index 0000000000000..fbd917ca343ee
--- /dev/null
+++ b/solution/3600-3699/3656.Determine if a Simple Graph Exists/README.md
@@ -0,0 +1,109 @@
+---
+comments: true
+difficulty: 中等
+edit_url: https://github.com/doocs/leetcode/edit/main/solution/3600-3699/3656.Determine%20if%20a%20Simple%20Graph%20Exists/README.md
+---
+
+
+
+# [3656. 判断是否存在简单图 🔒](https://leetcode.cn/problems/determine-if-a-simple-graph-exists)
+
+[English Version](/solution/3600-3699/3656.Determine%20if%20a%20Simple%20Graph%20Exists/README_EN.md)
+
+## 题目描述
+
+
+
+给定一个整数数组 degrees,其中 degrees[i] 表示第 i 个顶点的期望度数。
+
+你的任务是确定是否存在一个 恰好 具有这些顶点度数的 无向简单 图。
+
+一个 简单 图没有同一对顶点之间的自环或平行边。
+
+如果存在这样的图,返回 true,否则返回 false。
+
+
+
+示例 1:
+
+
+
输入:degrees = [3,1,2,2]
+
+
输出:true
+
+
解释:
+
+
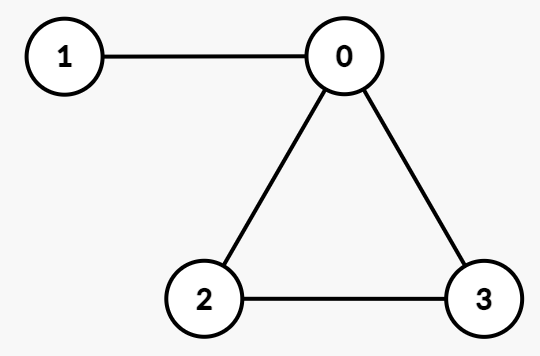
+
+
一个可能的无向简单图是:
+
+
+ - 边:
(0, 1), (0, 2), (0, 3), (2, 3)
+ - 度数:
deg(0) = 3,deg(1) = 1,deg(2) = 2,deg(3) = 2。
+
+
示例 2:
+
+
+
输入:degrees = [1,3,3,1]
+
+
输出:false
+
+
解释:
+
+
+ degrees[1] = 3 和 degrees[2] = 3 意味着它们必须连接到所有其他顶点。- 这需要
degrees[0] 和 degrees[3] 至少是 2,但它们都等于 1,这违反了需求。
+ - 因此,答案是
false。
+
+
+
+提示:
+
+
+ 1 <= n == degrees.length <= 1050 <= degrees[i] <= n - 1
+
+
+
+## 解法
+
+
+
+### 方法一
+
+
+
+#### Python3
+
+```python
+
+```
+
+#### Java
+
+```java
+
+```
+
+#### C++
+
+```cpp
+
+```
+
+#### Go
+
+```go
+
+```
+
+
+
+
+
+
diff --git a/solution/3600-3699/3656.Determine if a Simple Graph Exists/README_EN.md b/solution/3600-3699/3656.Determine if a Simple Graph Exists/README_EN.md
new file mode 100644
index 0000000000000..8a8a24fef29ad
--- /dev/null
+++ b/solution/3600-3699/3656.Determine if a Simple Graph Exists/README_EN.md
@@ -0,0 +1,107 @@
+---
+comments: true
+difficulty: Medium
+edit_url: https://github.com/doocs/leetcode/edit/main/solution/3600-3699/3656.Determine%20if%20a%20Simple%20Graph%20Exists/README_EN.md
+---
+
+
+
+# [3656. Determine if a Simple Graph Exists 🔒](https://leetcode.com/problems/determine-if-a-simple-graph-exists)
+
+[中文文档](/solution/3600-3699/3656.Determine%20if%20a%20Simple%20Graph%20Exists/README.md)
+
+## Description
+
+
+
+You are given an integer array degrees, where degrees[i] represents the desired degree of the ith vertex.
+
+Your task is to determine if there exists an undirected simple graph with exactly these vertex degrees.
+
+A simple graph has no self-loops or parallel edges between the same pair of vertices.
+
+Return true if such a graph exists, otherwise return false.
+
+
+Example 1:
+
+
+
Input: degrees = [3,1,2,2]
+
+
Output: true
+
+
Explanation:
+
+

+
+
One possible undirected simple graph is:
+
+
+ - Edges:
(0, 1), (0, 2), (0, 3), (2, 3)
+ - Degrees:
deg(0) = 3, deg(1) = 1, deg(2) = 2, deg(3) = 2.
+
+
Example 2:
+
+
+
Input: degrees = [1,3,3,1]
+
+
Output: false
+
+
Explanation:
+
+
+ degrees[1] = 3 and degrees[2] = 3 means they must be connected to all other vertices.- This requires
degrees[0] and degrees[3] to be at least 2, but both are equal to 1, which contradicts the requirement.
+ - Thus, the answer is
false.
+
+
+Constraints:
+
+
+ 1 <= n == degrees.length <= 1050 <= degrees[i] <= n - 1
+
+
+
+## Solutions
+
+
+
+### Solution 1
+
+
+
+#### Python3
+
+```python
+
+```
+
+#### Java
+
+```java
+
+```
+
+#### C++
+
+```cpp
+
+```
+
+#### Go
+
+```go
+
+```
+
+
+
+
+
+
diff --git a/solution/3600-3699/3656.Determine if a Simple Graph Exists/images/screenshot-2025-08-13-at-24347-am.png b/solution/3600-3699/3656.Determine if a Simple Graph Exists/images/screenshot-2025-08-13-at-24347-am.png
new file mode 100644
index 0000000000000..37c09ca697309
Binary files /dev/null and b/solution/3600-3699/3656.Determine if a Simple Graph Exists/images/screenshot-2025-08-13-at-24347-am.png differ
diff --git a/solution/README.md b/solution/README.md
index f3444add32b35..7f7bfb54d8c9e 100644
--- a/solution/README.md
+++ b/solution/README.md
@@ -3666,6 +3666,7 @@
| 3653 | [区间乘法查询后的异或 I](/solution/3600-3699/3653.XOR%20After%20Range%20Multiplication%20Queries%20I/README.md) | | 中等 | 第 463 场周赛 |
| 3654 | [删除可整除和后的最小数组和](/solution/3600-3699/3654.Minimum%20Sum%20After%20Divisible%20Sum%20Deletions/README.md) | | 中等 | 第 463 场周赛 |
| 3655 | [区间乘法查询后的异或 II](/solution/3600-3699/3655.XOR%20After%20Range%20Multiplication%20Queries%20II/README.md) | | 困难 | 第 463 场周赛 |
+| 3656 | [判断是否存在简单图](/solution/3600-3699/3656.Determine%20if%20a%20Simple%20Graph%20Exists/README.md) | | 中等 | 🔒 |
## 版权
diff --git a/solution/README_EN.md b/solution/README_EN.md
index d4c7c90102062..73286191323dd 100644
--- a/solution/README_EN.md
+++ b/solution/README_EN.md
@@ -3664,6 +3664,7 @@ Press Control + F(or Command + F on
| 3653 | [XOR After Range Multiplication Queries I](/solution/3600-3699/3653.XOR%20After%20Range%20Multiplication%20Queries%20I/README_EN.md) | | Medium | Weekly Contest 463 |
| 3654 | [Minimum Sum After Divisible Sum Deletions](/solution/3600-3699/3654.Minimum%20Sum%20After%20Divisible%20Sum%20Deletions/README_EN.md) | | Medium | Weekly Contest 463 |
| 3655 | [XOR After Range Multiplication Queries II](/solution/3600-3699/3655.XOR%20After%20Range%20Multiplication%20Queries%20II/README_EN.md) | | Hard | Weekly Contest 463 |
+| 3656 | [Determine if a Simple Graph Exists](/solution/3600-3699/3656.Determine%20if%20a%20Simple%20Graph%20Exists/README_EN.md) | | Medium | 🔒 |
## Copyright

