Fortran task 2 - FFT

Source files:

There are 2 source files, they are both in src folder:

• signals_sum.F90 - file responsible for changing given function into the sum of signals
• noise_deleting.F90 - file responsible for second part of the task

There is also a Makefile in src folder, which contains following commands: build run_sum run_filter clean

Running instruction

In order to run the project, you need to have Intel Fortran Compiler (ifort) installed.

1. Clone the repository

2. Go to src directory and enter following command in terminal: make build. This command allows you to build project - both signals_sum and noise_delete files will be built.

3. To run first part of the task, enter following command in terminal: make run_sum.

4. To run second part of the task, enter following command in terminal: make run_filter.

5. If you type either make run_sum command or make run_filter command, results for both of them will be stored in res directory. If you want to do it, delete previous ones from this directory, as they won't be overwritten, but additional lines will be added to them.

Results and conclusions

Results for the first part of the task:

Changing signal into the sum of signals.

I used following function: x = sin(2 ∗ π ∗ t ∗ 200) + 2 ∗ sin(2 ∗ π ∗ t ∗ 400)

Following image represents the result of this task: There are two bars on the plot that represent maximum amplitude for given frequency. For function: x = sin(2 ∗ π ∗ t ∗ 200) + 2 ∗ sin(2 ∗ π ∗ t ∗ 400) there are two components, so there are two bars as well.

Results for the second part of the task

Next task was to create garbled cosinus function. Mine was: cos(2 * pi * t * 4) + (random_noise - 1) * 0.1 where (random_noise - 1) * 0.1 is just some small distortion added to the cosinus. Following image presents this garbled cosinus:

Next part of the task was to perform Fourier Transform on the signal. Following image presents results of this operation:

Then I had to filter given fourier transform - delete values for which the amplitude was smaller than 50. Following image presents results of this operation:

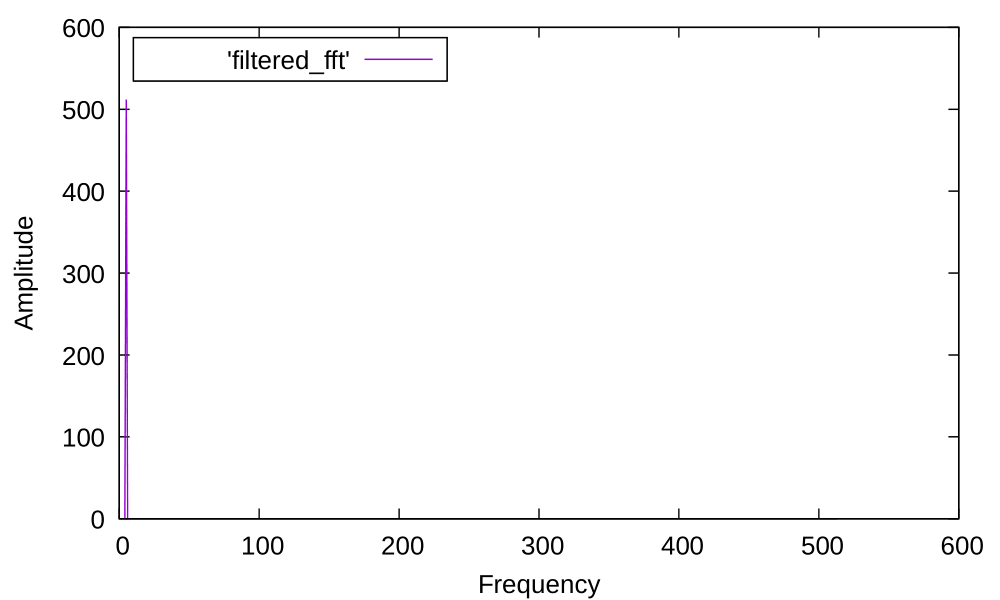
Final part of the task was to perform Inverse Fourier Transform on the part that was filtered. Following image presents results of this operation:

All foregoing plots are available in res, both png and pdf files.

All commands that I used in order to create plots using gnuplot are also available in res directory.