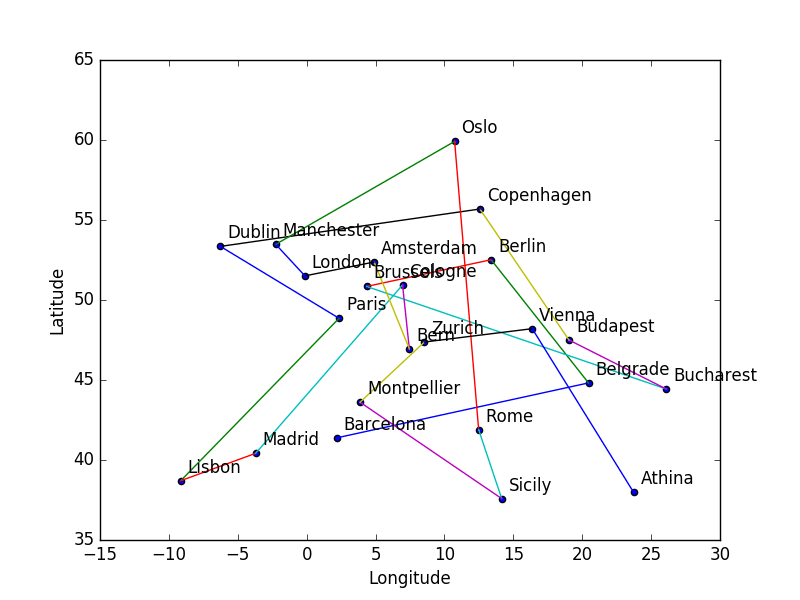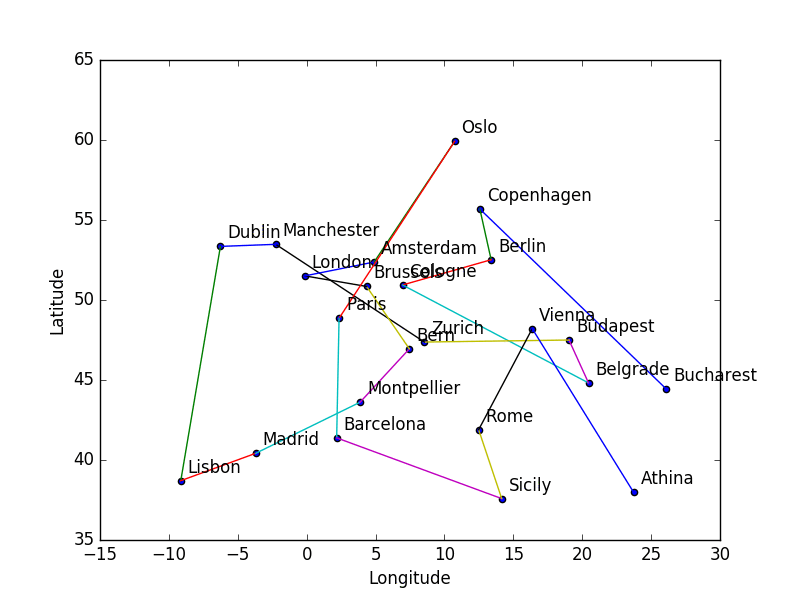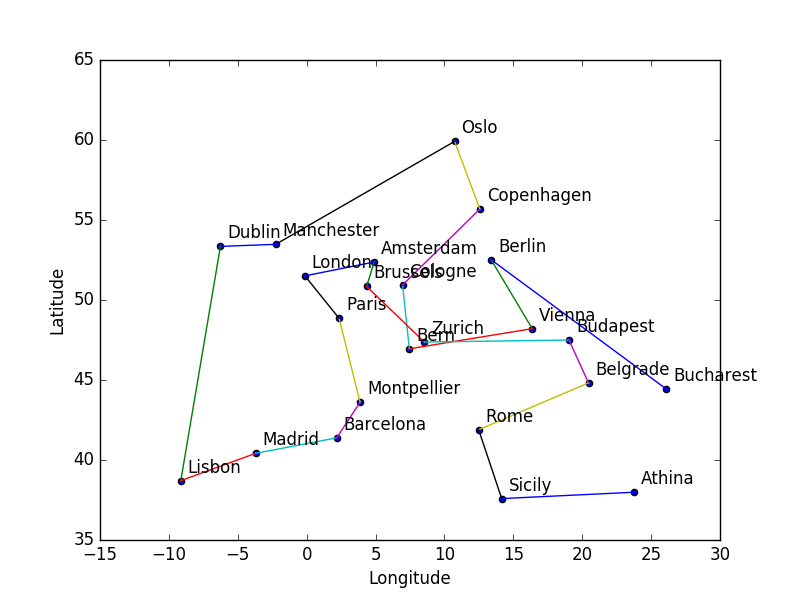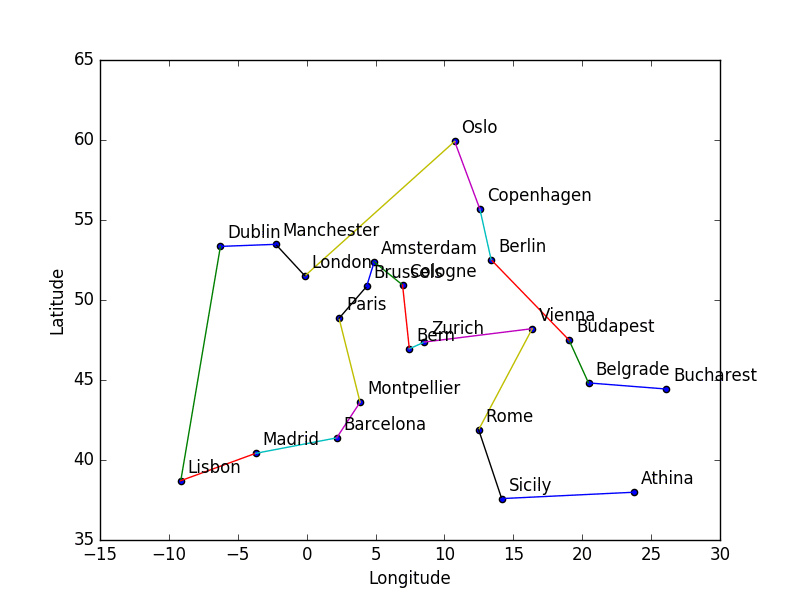
The goal of this repository is to apply Simulated Annealing to a Traveling Salesman Problem. Given a set of cities in Europe, the algorithm determines an approximately optimal route using Simulated Annealing.
The energy function here is based solely on the total distance of a given journey (depending on the order of cities).
def energy(self, trip):
return self.journey_distance(trip)
def journey_distance(self, trip, round_trip=True):
assert self.distances is not None, 'No distance matrix loaded'
distances = []
if round_trip:
for i in range(len(trip)-1):
distances.append(self.distances.loc[trip[i]].loc[trip[i+1]])
return np.array(distances).sum()
The script receives an input of city names as strings
t = TravelingTourist()
t.define_problem(['Barcelona', 'Belgrade', 'Berlin', 'Brussels', 'Bucharest', 'Budapest', 'Copenhagen', 'Dublin', 'Paris', 'Lisbon', 'Madrid', 'Cologne', 'Bern', 'Amsterdam', 'London', 'Manchester', 'Oslo', 'Rome', 'Sicily', 'Montpellier', 'Zurich', 'Vienna', 'Athina'])
which are written either in English or in the language of the country.
Using geopy, I collect the latitudes and longitudes and calculate the distance between the cities using Vincenty distance (appropriate distance for points on a sphere). These are saved in self.distances and self.latlong respectively.
t.make_distances()
t.make_latlong()
Alternatively, these matrices can also be saved and loaded directly from file
t.make_distances(load_from_file='distance_matrix.csv')
t.make_latlong(load_from_file='latlong_matrix.csv')
The annealing method is executed with a simple
t.anneal()
and its results are returned or can alternatively be viewed calling
t.trip
All states considered during the algorithm remain in
t.state_evolution