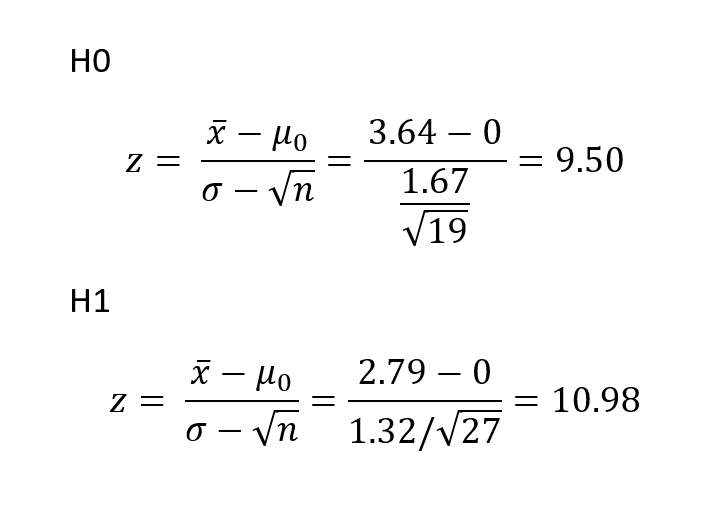P2_Probstat_C_5025201272

Praktikum PROBSTAT 2022 Modul 2

Sarah Alissa Putri - 5025201272

Soal 1

a. Carilah Standar Deviasi dari data selisih pasangan pengamatan tabel Untuk mencari standar deviasi, gunakan sd. Pertama, masukan data sebelum ke X dan sesudah ke Y menggunakan c(). Untuk mengetahui standar deviasinya, gunakan sd(X) dan sd(Y) untuk masing-masing variabel. Kemudian, gunakan sd(Y-X) atah sd(X-Y) untuk mencari nilai selisihnya.

#data sebelum
X <- c(78, 75, 67, 77, 70, 72, 78, 74, 77)
#data sesudah
Y <- c(100, 95, 70, 90, 90, 90, 89, 90, 100)

sd(X)
sd(Y)

#selisih (bisa sd(X-Y) juga, hasilnya sama)
sd(Y-X)

Output :

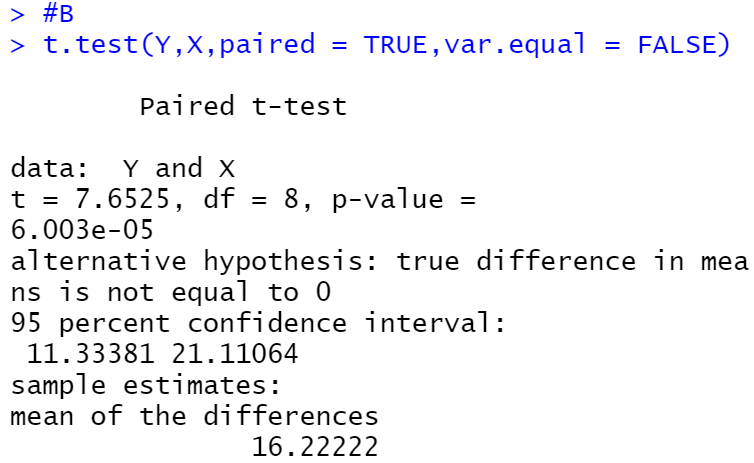
b. Carilah nilai t (p-value) Pada t.test(), nilai dari paired bernilai TRUE karena data X dan Y adalah sepasang. Selain itu, nilai dari var.equal adalah FALSE karena variabel X dan variabel Y memiliki varians yang berbeda.

t.test(Y,X,paired = TRUE,var.equal = FALSE)

Output :

c. Tentukanlah apakah terdapat pengaruh yang signifikan secara statistika dalam hal kadar saturasi oksigen , sebelum dan sesudah melakukan aktivitas 𝐴 jika diketahui tingkat signifikansi 𝛼 = 5% serta H0 : “tidak ada pengaruh yang signifikan secara statistika dalam hal kadar saturasi oksigen , sebelum dan sesudah melakukan aktivitas 𝐴”

Karena didapatkan p-value sebesar 6.003e-05 yang mengakibatkan H0 ditolak dan hipotesis alternatif diterima. Hal ini berarti terdapat pengaruh yang signifikan secara statistika dalam hal kadar saturasi oksigen, sebelum dan sesudah melakukan aktivitas A.

Soal 2

Diketahui bahwa mobil dikemudikan rata-rata lebih dari 20.000 kilometer per tahun. Untuk menguji klaim ini, 100 pemilik mobil yang dipilih secara acak diminta untuk mencatat jarak yang mereka tempuh. Jika sampel acak menunjukkan rata-rata 23.500 kilometer dan standar deviasi 3900 kilometer.

a. Apakah anda setuju dengan klaim tersebut? Setuju

b. Jelaskan maksud dari output yang dihasilkan!

Diketahui n = 100, Rata-Rata (X̄) = 23500, dan standar deviasi(σ) = 3900, sehingga dari hasil output didapatkan nilai z = 8.9744,p-value = 1, null hipotesisnya adalah H0 : μ = 20000 dan alternatif hipotesisnya adalah H1 : μ > 20000.

c. Buatlah kesimpulan berdasarkan P-Value yang dihasilkan!

P(Z > 8.9744) = 1 - P(Z < 8.9744)
= 1 - 1
= 0

Kesimpulan : Hipotesis awal (H0) bahwa "Mobil dikemudikan rata-rata lebih dari 20.000 kilometer per tahun" diterima.

Soal 3

Berilah keputusan serta kesimpulan yang didapatkan dari hasil diatas. Asumsikan nilai variancenya sama, apakah ada perbedaan pada rata-ratanya (α= 0.05)?

a. H0 dan H1

b. Hitung sampel statistik

tsum.test(mean.x = 3.64, s.x = 1.67, n.x = 19, mean.y = 2.79 , s.y = 1.32, n.y = 27, alternative = "greater", var.equal = TRUE)

c. Lakukan Uji Statistik (df =2)

install.packages("mosaic")
library(mosaic)

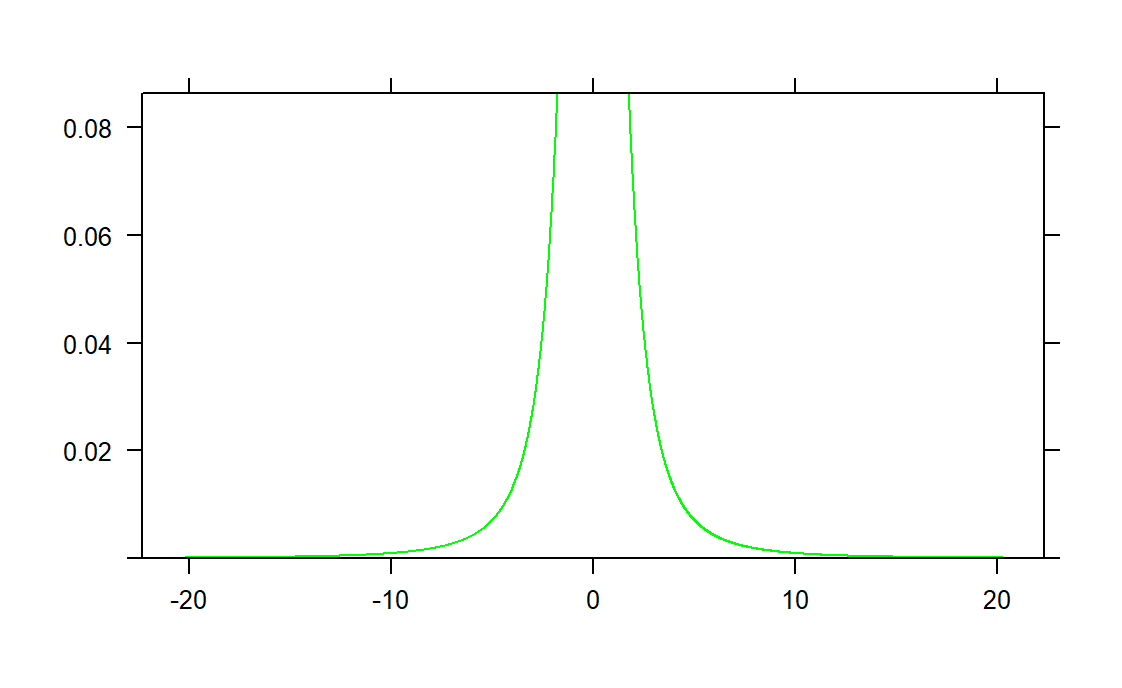
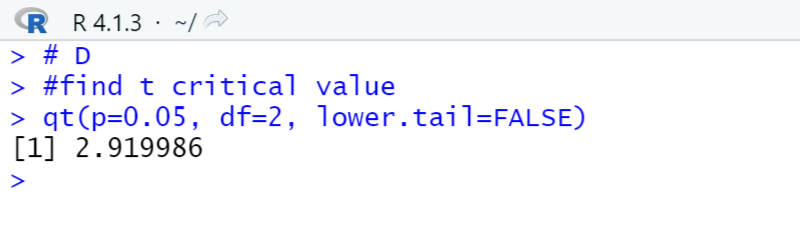
plotDist(dist = 't', df = 2, col = "green")

d. Nilai Kritikal Untuk mendapatkakn nilai kritikal, gunakan qt dengan df = 2 sesuai dengan soal 3C

qt(p=0.05, df=2, lower.tail=FALSE)

Output :

e. Keputusan

Dari hasil t-test didapatkan p-value = 0.03024 < 0.05. Maka H0 ditolak.

f. Kesimpulan

Kesimpulannya terdapat perbedaan antara rata-rata saham bandung dengan rata-rata saham bali.

Soal 4

Seorang Peneliti sedang meneliti spesies dari kucing di ITS . Dalam penelitiannya ia mengumpulkan data tiga spesies kucing yaitu kucing oren, kucing hitam dan kucing putih dengan panjangnya masing-masing. Jika : diketahui dataset https://intip.in/datasetprobstat1 H0 : Tidak ada perbedaan panjang antara ketiga spesies atau rata-rata panjangnya sama

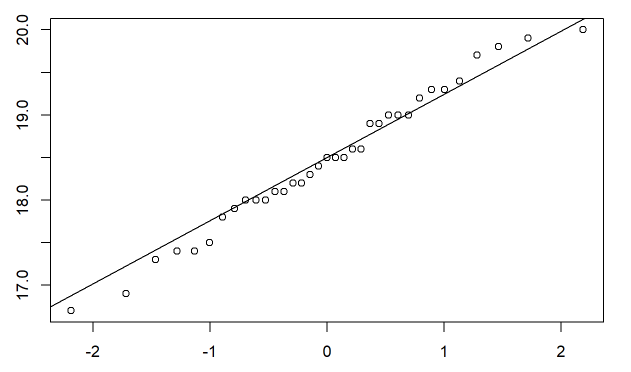
a. Buatlah masing masing jenis spesies menjadi 3 subjek "Grup" (grup 1,grup 2,grup 3). Lalu Gambarkan plot kuantil normal untuk setiap kelompok dan lihat apakah ada outlier utama dalam homogenitas varians.

Import data dari url dengan read.table(url()). Kemudian dilakukan pengelompokan berdasarkan Group yang terdiri atas 3 jenis yaitu "Kucing Oren","Kucing Hitam","Kucing Putih","Kucing Oren".

oneWayData  <- read.table(url("https://rstatisticsandresearch.weebly.com/uploads/1/0/2/6/1026585/onewayanova.txt"))
dim(oneWayData)
head(oneWayData)
attach(oneWayData)

oneWayData$Length <- as.factor(oneWayData$V2)
oneWayData$Group <- as.factor(oneWayData$V1)
oneWayData$Group = factor(oneWayData$Group,labels = c("Kucing Oren","Kucing Hitam","Kucing Putih","Kucing Oren"))
class(oneWayData$Group)

Kemudian simpan pengelompokan data dalam 3 variabel yang berbeda.

grup1 <- subset(oneWayData, Group == "Kucing Oren")
grup2 <- subset(oneWayData, Group == "Kucing Hitam")
grup3 <- subset(oneWayData, Group == "Kucing Putih")

Lakukan penggambaran plot kuantil normal untuk setiap kelompok.

ggplot(
  data = grup1,
  aes(sample = Length)
  ) + geom_qq()

ggplot(
  data = grup2,
  aes(sample = Length)
  ) + geom_qq()

ggplot(
  data = grup3,
  aes(sample = Length)
  ) + geom_qq()

b. Carilah atau periksalah Homogeneity of variances nya, Berapa nilai p yang didapatkan? , Apa hipotesis dan kesimpulan yang dapat diambil?

bartlett.test(oneWayData$Group, oneWayData$Length)

Diperoleh hasil sebagai berikut: bartlett = 0.43292 p-value = 0.8054

c. Untuk uji ANOVA (satu arah), buatlah model linier dengan Panjang versus Grup dan beri nama model tersebut model 1.

qqnorm(grup1$Length)
qqline(grup1$Length)

Output :

d. Dari Hasil Poin C, Berapakah nilai-p ? , Apa yang dapat Anda simpulkan dari H0?

Dari hasil poin c, p value = 0.8054, p value > 0.05. Kesimpulannya, H0 diterima.

e. Verifikasilah jawaban model 1 dengan Post-hoc test Tukey HSD, dari nilai p yang didapatkan apakah satu jenis kucing lebih panjang dari yang lain?

model <- lm(Length~Group, data = oneWayData)
anova(model)
TukeyHSD(aov(model))

Jika p-value lebih kecil dari 0.05, maka panjang kedua grup berbeda, jika p-value lebih dari 0.05 maka panjangnya sama. Berdasarkan hasil diatas dapat disimpulkan kucing putih dan kucing oren memiliki ukuran atau panjang yang sama.

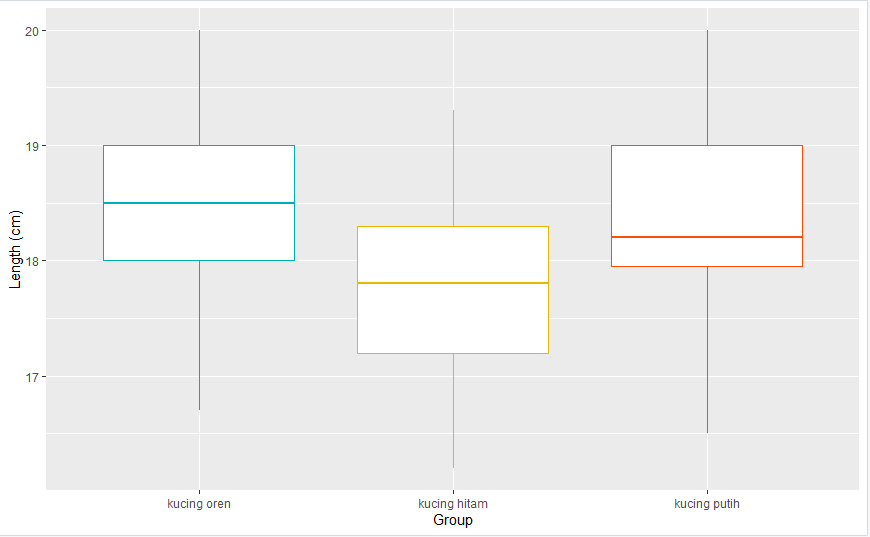
f. Visualisasikan data dengan ggplot2

ggplot(oneWayData, aes(x = Group, y = Length)) +
  geom_boxplot(color = c("#00AFBB", "#E7B800", "#FC4E07")) +
  scale_x_discrete() + xlab("Group") + ylab("Length (cm)")

Soal 5

Data yang digunakan merupakan hasil eksperimen yang dilakukan untuk mengetahui pengaruh suhu operasi (100˚C, 125˚C dan 150˚C) dan tiga jenis kaca pelat muka (A, B dan C) pada keluaran cahaya tabung osiloskop. Percobaan dilakukan sebanyak 27 kali dan didapat data sebagai berikut: Data Hasil Eksperimen. Dengan data tersebut:

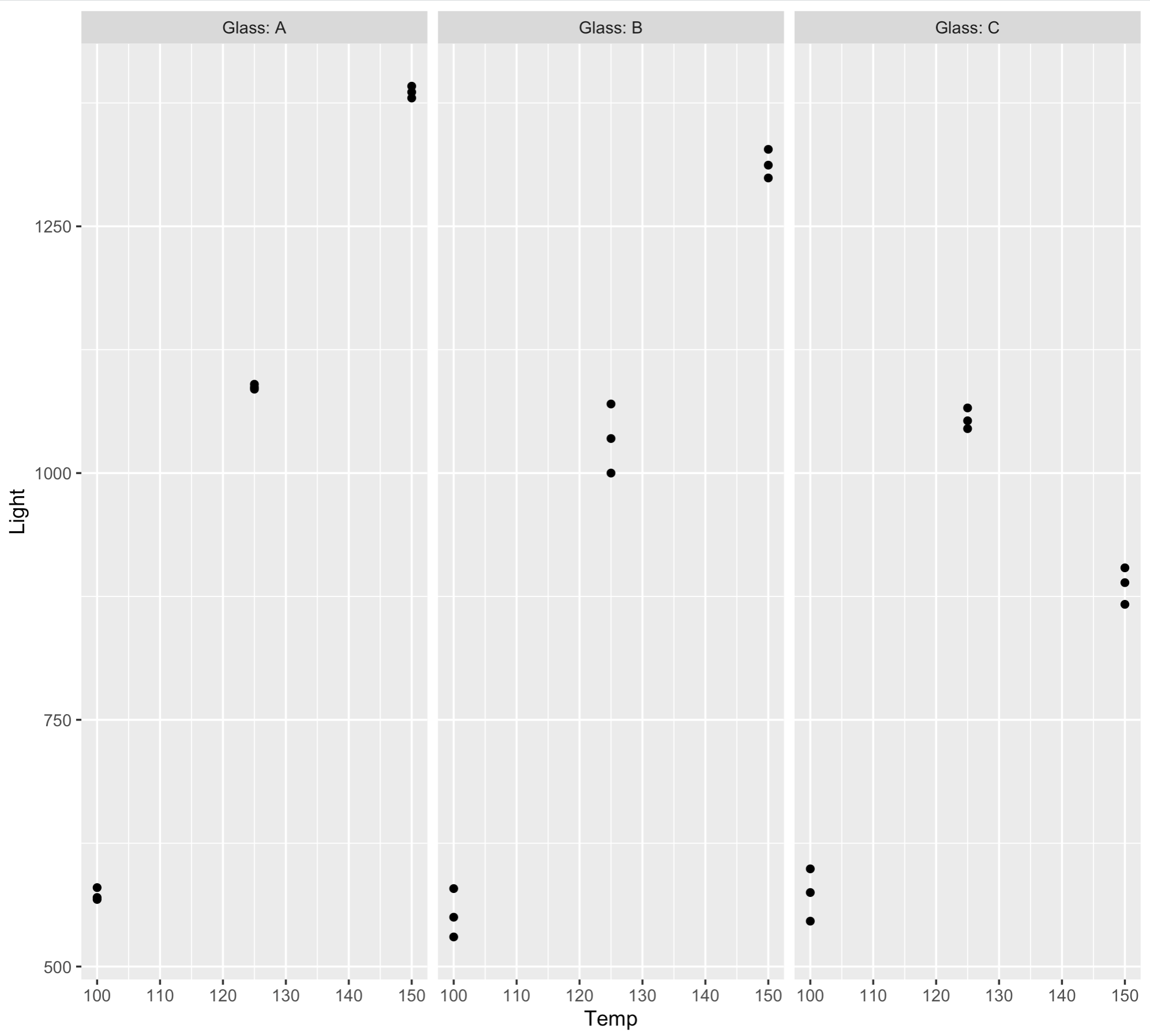
a. Buatlah plot sederhana untuk visualisasi data

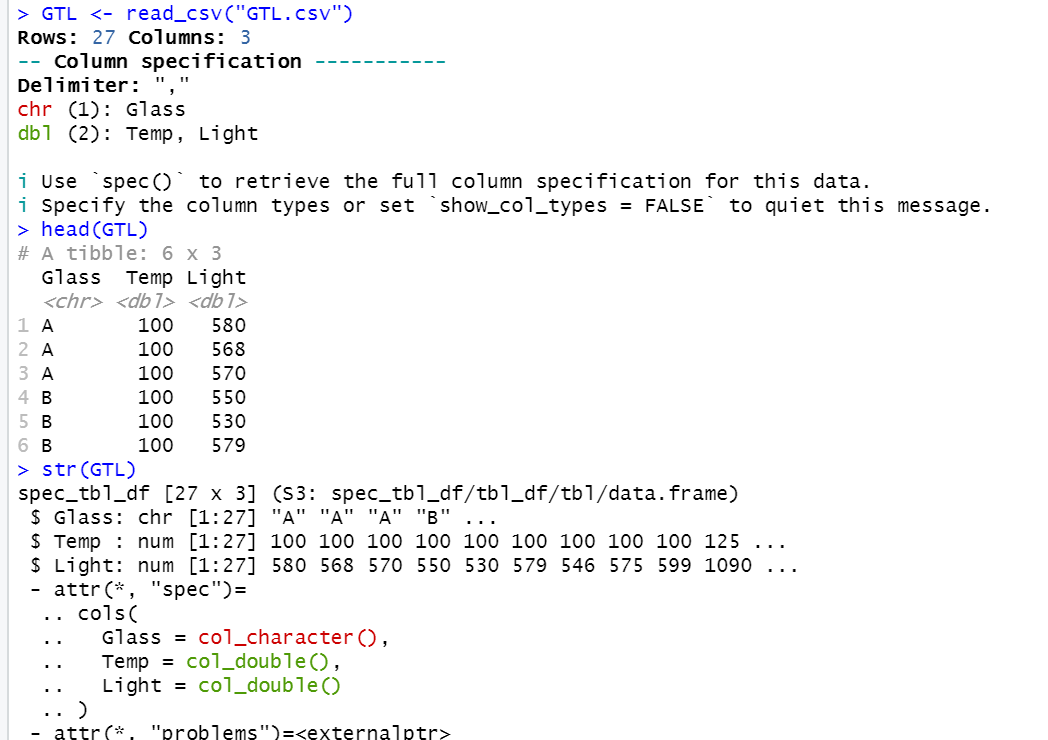
GTL <- read_csv("GTL.csv")
head(GTL)

str(GTL)

Output :

Lakukan visualisasi.

qplot(x = Temp, y = Light, geom = "point", data = GTL) +
  facet_grid(.~Glass, labeller = label_both)

b. Lakukan uji ANOVA dua arah

Buat variabel as factor sebagai ANOVA. Kemudian lakukan analisis of variance.

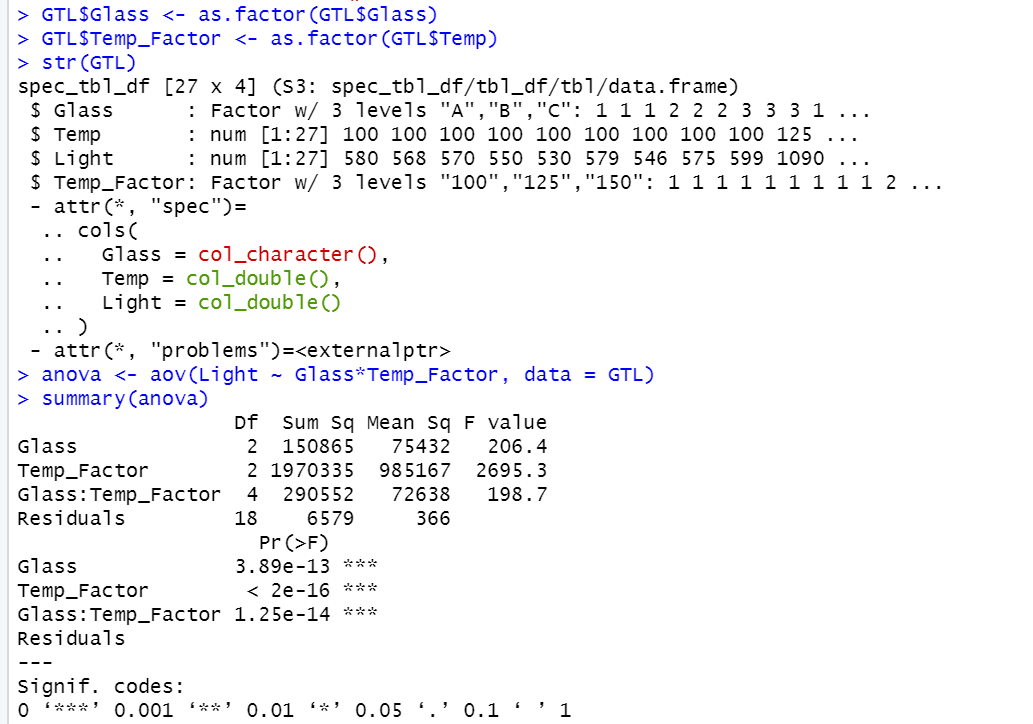
GTL$Glass <- as.factor(GTL$Glass)
GTL$Temp_Factor <- as.factor(GTL$Temp)
str(GTL)

anova <- aov(Light ~ Glass*Temp_Factor, data = GTL)
summary(anova)

c. Tampilkan tabel dengan mean dan standar deviasi keluaran cahaya untuk setiap perlakuan (kombinasi kaca pelat muka dan suhu operasi)

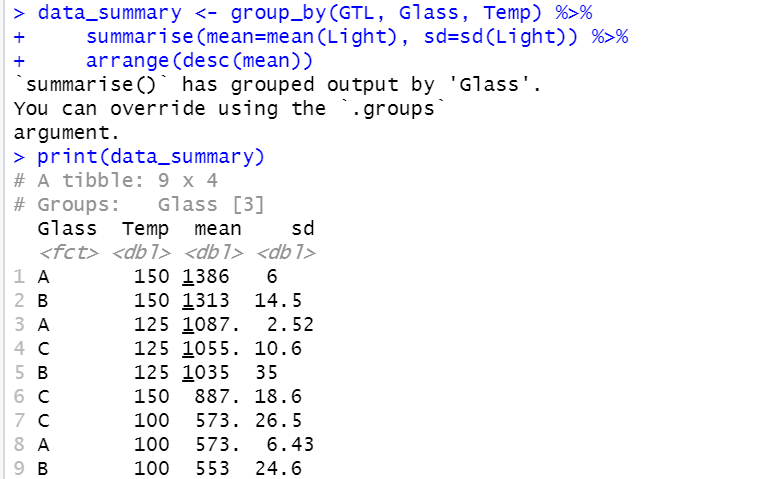
data_summary <- group_by(GTL, Glass, Temp) %>%
  summarise(mean=mean(Light), sd=sd(Light)) %>%
  arrange(desc(mean))
print(data_summary)

d. Lakukan uji Tukey

tukey <- TukeyHSD(anova)
print(tukey)

e. Gunakan compact letter display untuk menunjukkan perbedaan signifikan antara uji Anova dan uji Tukey

Compact letter display.

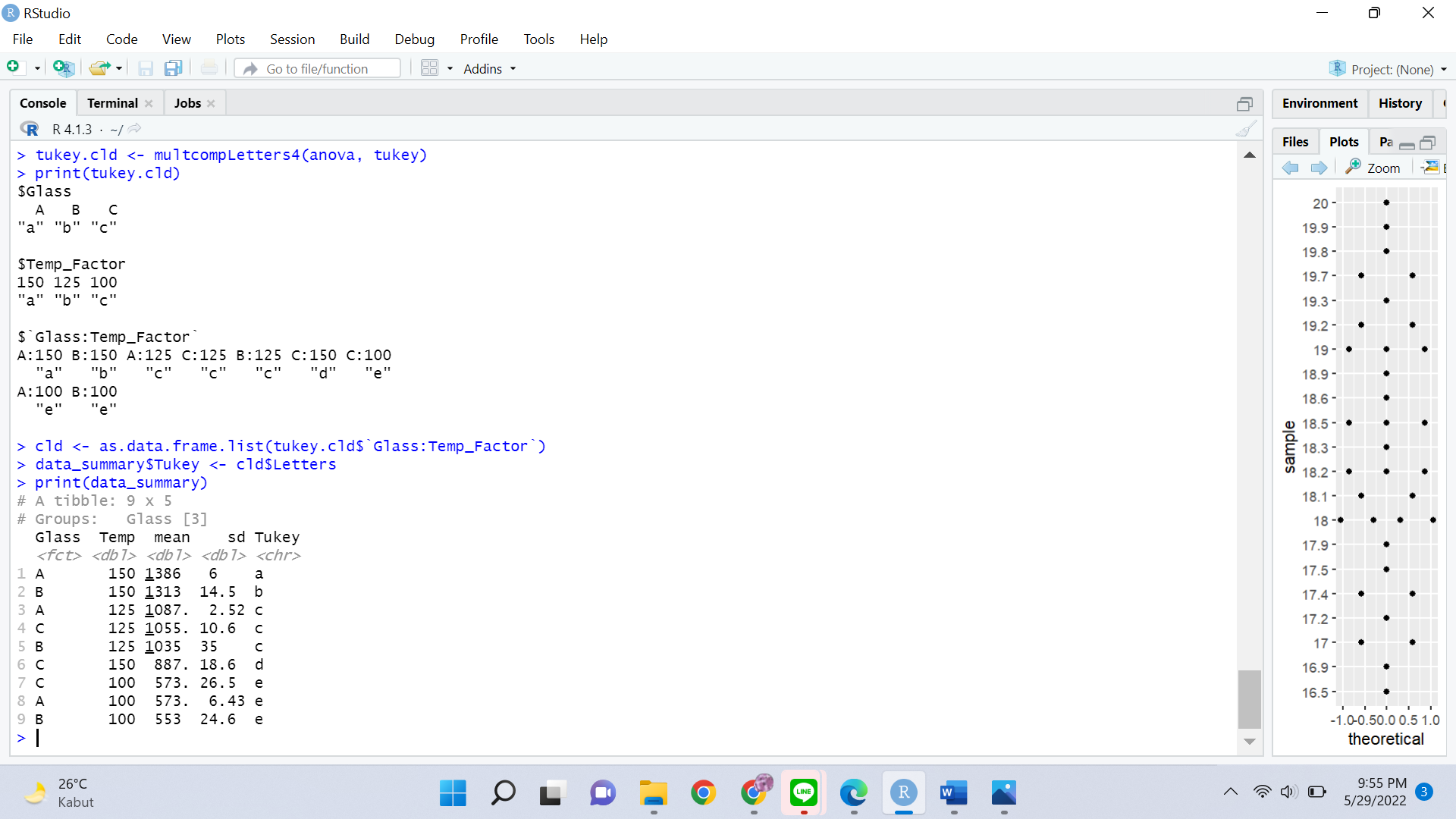
tukey.cld <- multcompLetters4(anova, tukey)
print(tukey.cld)

Tambahkan compact letter display tersebut ke tabel dengan means(rata-rata) dan sd.

cld <- as.data.frame.list(tukey.cld$`Glass:Temp_Factor`)
data_summary$Tukey <- cld$Letters
print(data_summary)